留数定理の例題【実積分への応用など】

この記事では、次の留数定理を用いた積分の例題と応用を扱います。

留数定理
関数 $f(z)$ は単純閉曲線 $C$ の内部に孤立特異点 $a_1,\cd,a_n$ を持つほかは $C$ の内部と周上をこめて正則とする. このとき, $$ \int_Cf(z)dz=2\pi i\sum_{k=1}^n\Res(f(z),a_k) $$

▼ 証明

[証明]
$\newcommand{\d}{\partial}$ $C$ 内部を $D$ とする. $a_k$ を中心として半径 $r$ の円 $B_r(a_k)$ について, 次を満たすように $r$ を十分小さくとる：
$$\eq{ & \ol{B_r(a_k)}\sub D, \\ j\neq k & \te{ならば} \ol{B_r(a_j)}\cap \ol{B_r(a_k)}=\emp. }$$ さて, コーシーの積分定理を $$ D\sm \bigcup_{k=1}^n\ol{B_r(a_k)} $$ に適用することにより $$ \int_{\d D}f(z)dz =\sum_{k=1}^n\int_{\d B_r(a_k)}f(z)dz =2\pi i\sum_{k=1}^n \Res(f(z),a_k) $$ を得る.

留数定理による積分計算

複素積分

例題
次の積分を求めよ.
$\ds\int_{|z|=5}\f{e^z}{(z-2)(z-4)}dz$

▼ 解答

[解答]
単純閉曲線 $|z|=5$ の内部にある, 関数 $f(z)=\f{e^z}{(z-2)(z-4)}$ の孤立特異点は $2,4$ であり, すべて位数１の極なので, それぞれの留数は $$\eq{ & \Res(f(z),2)=\lim_{z\to 2}(z-2)f(z) =\lim_{z\to 2}\f{e^z}{z-4}=-\f{e^2}{2} \\ & \Res(f(z),4)=\lim_{z\to 4}(z-4)f(z) =\lim_{z\to 4}\f{e^z}{z-2}=\f{e^4}{2} }$$ である. したがって, 留数定理によって, $$\eq{ \int_{|z|=5}f(z)dz & =2\pi i \Big( \Res(f(z),2)+\Res(f(z),4) \Big) \\ & =2\pi i\le(-\f{e^2}{2}+\f{e^4}{2} \ri) =\pi i(e^4-e^2). }$$

例題
次の積分を求めよ.
$\ds\int_{|z|=5}\f{2z}{(z-1)(z-2)(z-3)}dz$

▼ 解答

[解答]
単純閉曲線 $|z|=5$ の内部にある, 関数 $f(z)=\f{2z}{(z-1)(z-2)(z-3)}$ の孤立特異点は $1,2,3$ であり, すべて位数１の極なので, それぞれの留数は $$\eq{ & \Res(f(z),1)=\lim_{z\to 1}(z-1)f(z) =\lim_{z\to 1}\f{2z}{(z-2)(z-3)}=1 \\ & \Res(f(z),2)=\lim_{z\to 2}(z-2)f(z) =\lim_{z\to 2}\f{2z}{(z-1)(z-3)}=-4 \\ &\Res(f(z),3)=\lim_{z\to 3}(z-3)f(z) =\lim_{z\to 3}\f{2z}{(z-1)(z-2)}=3 }$$ である. したがって, 留数定理によって, $$\eq{ \int_{|z|=5}f(z)dz & =2\pi i \Big( \Res(f(z),1)+\Res(f(z),2)+\Res(f(z),3) \Big) \\ & =2\pi i(1-4+3)=0. }$$

実積分への応用

例題
次の積分を求めよ.
$\ds\int_{-\iy}^\iy\f{1}{x^2+1}dx$

▼ 解答

[解答]
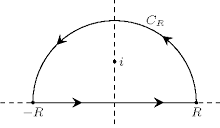$\ds f(z)=\f{1}{z^2+1}$ とする.
図のように, 十分大きな $R >0$ をとり, 半円の弧 $C_R:z=Re^{i\t}(0\leq \t\leq \pi)$ と閉区間 $I_R:=[-R,R]$ をつないで閉曲線 $C$ をつくる. このとき, $$ \int_Cf(z)dz=\int_{C_R}f(z)dz +\int_{I_R} f(z)dz \tag{*} $$ が成り立つ. $f(z)$ の孤立特異点は $i,-i$ の２つであり, そのうち閉曲線 $C$ の内部には $i$ だけがある. $i$ は $f(z)$ の一位の極なので, $$\eq{ \int_Cf(z)dz & =2\pi i\ \Res(f(z),i) \\ & =2\pi i\lim_{z\to i}(z-i)f(z) \\ & =2\pi i\c \f{1}{2i} \\ & =\pi }$$ $f(z)$ の $C_R$ に沿った積分は $$\eq{ \le| \int_{C_R}f(z)dz\ri| & \leq \int_{C_R}\le| \f{1}{z^2+1} \ri| |dz| \\ & \leq \int_{C_R}\f{1}{|z^2|-1}|dz| \\ & = \f{1}{R^2-1}\int_{C_R}|dz| \\ & = \f{\pi R}{R^2-1}\to 0\ \ \ (R\to\iy). }$$ また, $$ \int_{I_R} f(z)dz =\int_{-R}^R\f{1}{x^2+1}dx \to \int_{-\iy}^\iy\f{1}{x^2+1}dx\ \ \ (R\to \iy). $$ ゆえに, 式 $(*)$ において, $R\to \iy$ とすれば $$ \int_{-\iy}^\iy\f{1}{x^2+1}dx=\pi $$

例題
次の積分の値を求めよ.
$\ds\int_{-\iy}^\iy\f{1}{x^4+1}dx$

▼ 解答

[解答]
$\ds f(z)=\f{1}{z^4+1}$ とする.
図のように, 十分大きな $R >0$ をとり, 半円の弧 $C_R:z=Re^{i\t}(0\leq \t\leq \pi)$ と閉区間 $I_R:=[-R,R]$ をつないで閉曲線 $C$ をつくる. このとき, $$ \int_Cf(z)dz=\int_{C_R}f(z)dz +\int_{I_R} f(z)dz \tag{*} $$ が成り立つ. $z^4+1=0$ の解は $e^{\pi i/4},e^{3\pi i/4},e^{5\pi i/4},e^{7\pi i/4}$ であり, そのうち, 閉曲線 $C$ の内部には, $$\eq{ \a & :=e^{\pi i/4}=\f{1}{\r{2}}+i\f{1}{\r{2}} \\ \b & :=e^{3\pi i/4}=-\f{1}{\r{2}}+i\f{1}{\r{2}} }$$ の２つがある. $\a,\b$ は $f(z)$ の一位の極なので, 留数定理より, $$\eq{ \int_Cf(z)dz & =2\pi i(\Res(f(z),\a)+\Res(f(z),\b)) \\ & =2\pi i\le(\f{1}{4\a^3}+\f{1}{4\b^3}\ri) \\ & =2\pi i\le(\f{-\a}{4}+\f{-\b}{4}\ri) \\ & =\f{-\pi i}{2}(\a+\b) \\ & =\f{\pi}{\r{2}} }$$ となる. ここで, $\a^4=\b^4=-1$ を用いた. 一方, $$ \lim_{z\to\iy}|z^2f(z)| =\lim_{z\to\iy}\le| \f{z^2}{z^4+1} \ri| =\lim_{z\to\iy}\f{|z|^2}{|z^4+1|}=0 $$ であるから, $|z^2f(z)|\leq M$ を満たす実数 $M>0$ がとれる. したがって, $$\eq{ \le| \int_{C_R} f(z)dz \ri| & \leq \int_{C_R} |f(z)||dz| \leq \int_{C_R}\f{M}{|z|^2}|dz| \\ & =\f{M}{R^2}\int_{C_R}|dz| =\f{M\pi}{R}\to 0\ \ \ (R\to \iy) }$$ が成り立つ. また, $$ \int_{I_R} f(z)dz =\int_{-R}^R\f{1}{x^4+1}dx \to \int_{-\iy}^\iy\f{1}{x^4+1}dx\ \ \ (R\to \iy). $$ ゆえに, 式 $(*)$ において, $R\to \iy$ とすれば $$ \int_{-\iy}^\iy\f{1}{x^4+1}dx=\f{\pi}{\r{2}} $$

※留数の計算に次を用いた：
$f(z),g(z)$ が正則で $g(a)=0,g'(a)\neq 0$ のとき, $$ \Res\le(\f{f(z)}{g(z)},a\ri)=\f{f(a)}{g'(a)} $$

例題
次の積分の値を求めよ.
$\ds\int_0^\iy \f{x}{1+x^4}dx$

▼ 解答

[解答]
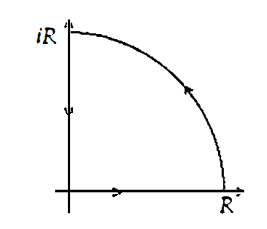被積分関数は奇関数なので, $-\iy$ から $\iy$ までの積分は０になる. なので, 半円を積分路としてもうまくいかない. 今回は図のように四分円(quarter circle)を積分路にする. $f(z) =\f{z}{1+z^4}$ とする. $f(z)$ は四分円内で一位の極 $e^{\pi i/4}$ をもち, その留数は $$ \le.\f{z}{(1+z^4)'} \ri|_{z=e^{\pi i/4}} =\le.\f{z}{4z^3} \ri|_{z=e^{\pi i/4}} =\f{e^{\pi i/4}}{4e^{3\pi i/4}} =\f{e^{-\pi i/2}}{4} =-\f{i}{4} $$ である. 留数定理より, $$\eq{ & \int_0^R \f{x}{1+x^4}dx + \int_0^{\pi/2}\f{Re^{i\t}}{1+(Re^{i\t})^4}iRe^{i\t}d\t + \int_R^0 \f{iy}{1+y^4}idy \\ = & 2\pi i \le(-\f{i}{4}\ri) = \f{\pi}{2}. \tag{*} }$$ 左辺真ん中の項は $R\to \iy$ のとき $0$ に収束する. また, $$ \int_0^R \f{x}{1+x^4}dx =\int_R^0 \f{iy}{1+y^4}idy $$ が成り立つことに注意しよう. したがって, $R\to \iy$ のとき, $(*)$ は $$ 2\int_0^\iy \f{x}{1+x^4}dx =\f{\pi}{2} $$ となる. よって, $$ \int_0^\iy \f{x}{1+x^4}dx =\f{\pi}{4} $$ を得る.

例題
次の積分の値を求めよ.
$\ds\int_{-\iy}^\iy \f{e^{ax}}{1+e^x}\ \ \ (0 < a< 1)$

▼ 解答

[解答]
まず, この広義積分が収束することは $$ \f{e^{ax}}{1+e^x} \sim e^{-(1-a)x} \te{as} x\to \iy, $$ $$ \f{e^{ax}}{1+e^x} \sim e^{ax} \te{as} x\to -\iy $$ からわかる. 複素関数 $f(z)=e^{az}/(1+e^z)$ と下図のような長方形の閉曲線を考える.

$f(z)$ は長方形内において $\pi i$ で一位の極をもち, その留数は $e^{a\pi i}/e^{\pi i}=-e^{a\pi i}$ である. 従って, $$\eq{ -2\pi i e^{a\pi i} & =\int_{-R}^R\f{e^{ax}}{1+e^x}dx +\int_0^{2\pi}\f{e^{a(R+iy)}}{1+e^{R+iy}}idy \\ & \ \ \ \ \ -\int_{-R}^R\f{e^{a(x+2\pi i)}}{1+e^{x+2\pi i}}dx -\int_0^{2\pi}\f{e^{a(-R+iy)}}{1+e^{-R+iy}}idy. \tag{*} }$$ 今, 十分大きい $R$ に対して, $$ \le| \f{e^{a(R+iy)}}{1+e^{R+iy}} \ri| \leq \f{e^{aR}}{e^R-1} \leq 2e^{-(1-a)R}. $$ したがって, $$ \le| \int_0^{2\pi}\f{e^{a(R+iy)}}{1+e^{R+iy}}i\ dy \ri| \leq 4\pi e^{-(1-a)R}, $$ は $R\to \iy$ のとき $0$ に収束する. 同様に, 十分大きい $R$ に対して, $$ \le| \f{e^{a(-R+iy)}}{1+e^{-R+iy}} \ri| \leq \f{e^{-aR}}{1-e^{-R}} \leq 2e^{-aR}. $$ したがって, $$ \le| \int_0^{2\pi}\f{e^{a(-R+iy)}}{1+e^{-R+iy}} i\ dy \ri| \leq 4\pi e^{-aR}, $$ は $R\to \iy$ のとき $0$ に収束する. また, $$ \int_{-R}^R \f{e^{a(x+2\pi i)}}{1+e^{x+2\pi i}}dx =e^{2a\pi i}\int_{-R}^R \f{e^{ax}}{1+e^x}dx. $$ したがって, $R\to \iy$ とすると, $(*)$ から $$ (1-e^{2a\pi i})\int_{-\iy}^\iy \f{e^{ax}}{1+e^x}dx =-2\pi ie^{a\pi i}. $$ ゆえに $$ \int_{-\iy}^\iy \f{e^{ax}}{1+e^x}dx =\f{2\pi i}{e^{a\pi i}-e^{-a\pi i}} =\f{\pi}{\sin a\pi}. $$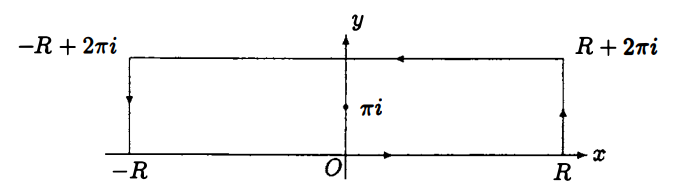

補足：
この積分に $x=\log t$ で置換すると, $$ \int_0^\iy \f{t^{a-1}}{1+t}dt $$ を得る. この積分はベータ関数 $B(a,1-a)$ に一致する. さらに, ベータ関数とゼータ関数の関係式から $$ B(a,1-a)=\G(a)\G(1-a) $$ が成り立つので, 恒等式 $$ \G(a)\G(1-a)=\f{\pi}{\sin a\pi}\ \ \ (0< a< 1) $$ を得る.

三角関数の定積分

例題
$a>1$ のとき, 次の積分の値を求めよ.
$\ds(1)\ \int_0^{2\pi}\f{1}{a+\cos\t}d\t \ \ \ \ \ \ \ \ \ (2)\ \int_0^{2\pi}\f{1}{a+\sin\t}d\t$

[解答]
【留数定理】三角関数の積分【例題】参照.

例題
$a>0$ のとき, 次の積分の値を求めよ.
$\ds(1)\ \int_0^{2\pi}\f{1}{a+\cos^2\t}d\t\ \ \ \ \ \ \ \ \ (2)\ \int_0^{2\pi}\f{1}{a+\sin^2\t}d\t$

[解答]
【留数定理】三角関数の積分【例題】参照.

例題
次を示せ. $$ \int_0^\iy \cos(x^2)dx=\int_0^\iy \sin(x^2)dx =\r{\pi/8} $$

[解答]
ジョルダンの補題【証明と応用】参照.

問題
次を示せ. $$ \int_0^\iy \f{\sin x}{x}dx =\f{\pi}{2} $$

[解答]
ジョルダンの補題【証明と応用】参照.