コーシーの積分定理【証明と例題】
この記事では、コーシーの積分定理を扱います。
コーシーの積分定理
定理
関数 $f(z)$ が閉曲線 $C$ およびその内部で正則であるとき,
次が成り立つ.
$$ \int_C f(z)dz=0 $$
[証明]
$f(z)=u(x,y)+iv(x,y)$ とする.
$C$ が $z=x(t)+iy(t)\ (a\leq t\leq b)$
で表されているとき,
$$\eq{
\int_C f(z)dz
& =\int_a^b\Big( u(x(t),y(t))+iv(x(t),y(t)) \Big)
\le(\f{dx}{dt}+i\f{dy}{dt}\ri) dt
\\ & =\int_a^b\le( u(x(t),y(t))\f{dx}{dt}
-v(x(t),y(t))\f{dy}{dt} \ri)dt
\\ & \ \ \ +i\int_a^b\le( v(x(t),y(t))\f{dx}{dt}
+u(x(t),y(t))\f{dy}{dt} \ri)dt
\\ & =\int_C(udx-vdy)+i\int_C(vdx+udy)
}$$
となる. したがって, 閉曲線 $C$ の内部を $D$ とすれば,
グリーンの定理より,
$$\eq{
\int_C f(z)dz
& =\int_C(udx-vdy)+i\int_C(vdx+udy)
\\ & =\iint_D\le(-\dd{u}{y}-\dd{v}{x}\ri)dxdy
+i\iint_D\le(-\dd{v}{y}+\dd{u}{x}\ri)dxdy
}$$
である. ここで, $f(z)$ は正則であるから, $u,v$
はコーシー・リーマンの関係式
$$ \dd{u}{x}=\dd{v}{y},\ \ -\dd{u}{y}=\dd{v}{x} $$
を満たす. よって,
$$ \int_C f(z)dz=0. $$
正則でない関数について
例
複素関数 $f(z)=\ol{z}$ は正則でない.
実際, $z=e^{i\t}$ とおくと, $dz=ie^{i\t}d\t$ より,
$$ \int_{|z|=1}f(z)dz
=\int_0^{2\pi}e^{-i\t}ie^{i\t}d\t
=\int_0^{2\pi}id\t=2\pi i.
$$
よって, $\int_{|z|=1}f(z)dz\neq 0$ より,
コーシーの積分定理は成り立たない.
例
複素関数 $\ds f(z)=\f{1}{z}$ は $z=0$ で正則でない.
実際, $z=e^{i\t}$ とおくと, $dz=ie^{i\t}d\t$ より,
$$ \int_{|z|=1}f(z)dz
=\int_0^{2\pi}\f{1}{e^{i\t}}ie^{i\t}d\t
=\int_0^{2\pi}id\t=2\pi i.
$$
よって, $\int_{|z|=1}f(z)dz\neq 0$ より,
コーシーの積分定理は成り立たない.
積分経路の取り方
コーシーの積分定理の応用として, 正則な関数の積分は, 積分経路によらず, 始点と終点で決まることがわかる.
定理
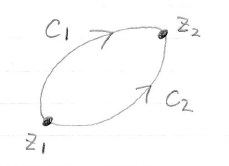$f(z)$ を領域 $D$ 上で正則な関数とし,
$z_1,z_2\in D$ とする.
$C_1,C_2$ を始点が $z_1,$ 終点が $z_2$ の曲線とする.
このとき,
$$ \int_{C_1} f(z)dz=\int_{C_2} f(z)dz $$
[証明]
$C_2$ の逆向きの経路 $(z_2 \te{から} z_1)$
を $-C_2$ と表すと, $C_1-C_2$ は $z_1\to z_2 \to z_1$
の閉じた閉曲線になる. よって, コーシーの積分定理より
$$ \int_{C_1-C_2} f(z)dz
=\int_{C_1} f(z)dz+\int_{-C_2} f(z)dz=0 $$
であるが,
$$\int_{-C_2} f(z)dz=-\int_{C_2} f(z)dz$$
であるので,
$$ \int_{C_1} f(z)dz=\int_{C_2} f(z)dz $$
定理
$C_1$ を閉曲線とし, $C_2$ を $C_1$ の内側にある閉曲線とする.
そして, $C_1$ と $C_2$ の間の領域では関数 $f(z)$
は正則であるとする. このとき,
$$ \int_{C_1} f(z)dz=\int_{C_2} f(z)dz $$
[証明]
$C_2$ の逆向きの経路 $(z_2 \te{から} z_1)$
を $-C_2$ と表すと, $C_1-C_2$ は $z_1\to z_2 \to z_1$
の閉じた閉曲線になる. よって, コーシーの積分定理より
$$ \int_{C_1-C_2} f(z)dz
=\int_{C_1} f(z)dz+\int_{-C_2} f(z)dz=0 $$
であるが,
$$\int_{-C_2} f(z)dz=-\int_{C_2} f(z)dz$$
であるので,
$$ \int_{C_1} f(z)dz=\int_{C_2} f(z)dz $$
応用
コーシーの積分公式
定理 (コーシーの積分公式)
$f(z)$ が正則であり, 点 $z=a$ が閉曲線 $C$ の内部にあるとき,
$$ f(a)=\f{1}{2\pi i}\int_C\f{f(z)}{z-a}dz $$
コーシーの積分定理は当初, 導関数 $f'(z)$ が「連続である」という条件が付いていた.
しかしÉdouard Goursatによって, 連続性の仮定をはずして,
導関数 $f'(z)$ が存在するという条件だけでコーシーの積分定理を証明した.
この結果は重要である.
なぜなら, この結果によって, 連続性の仮定なしのコーシーの積分公式を証明でき,
さらに, コーシーの積分公式から帰納法を用いて正則関数は無限回微分可能であることが導かれるからである.
詳しいことはコーシーの積分公式【証明と例題】を参照してほしい.
その他
・コーシーの積分定理はリーマン面に一般化できる.