コーシーの積分公式【証明と例題】

この記事では、
・コーシーの積分公式(Cauchy's integral theorem)
・グルサの定理(Goursat's theorem)
について証明と例題を扱います。

コーシーの積分公式

証明

コーシーの積分公式の証明にコーシーの積分定理を用います. (参照:コーシーの積分定理【証明と例題】)

定理 (コーシーの積分公式)
$f(z)$ を領域 $A$ 上で正則な関数とする.
$z_0$ が閉曲線 $C$ の内部の点ならば, $$ f(z_0)=\f{1}{2\pi i}\int_C\f{f(z)}{z-z_0}dz $$ が成り立つ.

▼ 証明

[証明]
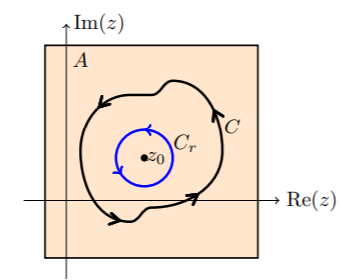$C_r$ を右図のように中心 $z_0,$ 半径 $r$ の円とする.
このとき, コーシーの積分定理より, $$ I=\int_C\f{f(z)}{z-z_0}dz =\int_{C_r}\f{f(z)}{z-z_0}dz. $$ ゆえに, 右辺の積分 $\ds\int_{C_r}$ は $r$ と関係ない一定の値 $I$ になる.
$f(x)$ は $A$ 上連続なので, 任意の $\e >0$ に対して, $r$ を十分小さくとれば, $C_r$ 上で $$ |f(z)-f(z_0)|< \e $$ が成り立つ. さて $$ I=\int_{C_r}\f{f(z)}{z-z_0}dz =f(z_0)\int_{C_r}\f{dz}{z-z_0} +\int_{C_r}\f{f(z)-f(z_0)}{z-z_0}dz $$ である. 右辺の第一の積分は $2\pi i f(z_0)$ に等しい. 第二の積分に関しては $$ \le| \int_{C_r}\f{f(z)-f(z_0)}{z-z_0}dz \ri| <\f{\e}{r}\int_{C_r} dz =\f{\e}{r}\c 2\pi r=2\pi\e. $$ すなわち $$ |I-2\pi if(z_0)|< 2\pi\e. $$ $\e$ は任意だから $$ I=2\pi if(z_0). $$

例題

例題
積分 $\ds\int_{|z|=2}\f{e^z}{z-1}dz$ の値を求めよ.

▼ 解答

[解答]
$f(z)=e^z$ とおくと $f(z)$ は複素平面全体で正則であり, 点 $z=1$ は円 $|z|=2$ の内部にある. したがって, コーシーの積分公式より, $$ \int_{|z|=2}\f{e^z}{z-1}dz =\int_{|z|=2}\f{f(z)}{z-1}dz=2\pi i f(1)=2\pi ie $$

例題
積分 $\ds\int_{|z|=1}\f{e^{iz}}{z}dz$ の値を求めよ.

▼ 解答

[解答]
$f(z)=e^{iz}$ とおくと $f(z)$ は複素平面全体で正則であり, 点 $z=0$ は円 $|z|=1$ の内部にある. したがって, コーシーの積分公式より, $$ \int_{|z|=1}\f{e^{iz}}{z}dz =2\pi i f(0)=2\pi i $$

例題
積分 $\ds\int_{|z|=1}\f{z^2+3}{z(z-2)}dz$ の値を求めよ.

▼ 解答

[解答]
$f(z)=\f{z^2+3}{z-2}$ とおく. 点 $z=2$ は円 $|z|=1$ の外部にあるから, $f(z)$ は $|z|=1$ およびその内部で正則である. 被積分関数は $$ \f{z^2+3}{z(z-2)}=\f{f(z)}{z} $$ と変形できるから, コーシーの積分公式より, $$ \int_{|z|=1}\f{z^2+3}{z(z-2)}dz =\int_{|z|=1}\f{f(z)}{z}dz =2\pi i f(0)=2\pi i \c \le(-\f{3}{2}\ri)=-3\pi i $$

例題
コーシーの積分公式を使って以下の積分の値を求めよ.
$$ I=\int_C\f{e^z}{z-2}dz \ \ \ (C \te{は} z=2 \te{を中心とした円}) $$

▼ 解答

[解答]
被積分関数の特異点は２であり, $C$ の内部にある. コーシーの積分公式より $$ e^2=\f{1}{2\pi i}\int_C\f{e^z}{z-2}dz =\f{I}{2\pi i} $$ となる. よって, $I=2\pi i e^2$ である.

例題
コーシーの積分公式を使って以下の積分の値を求めよ.
$$ I=\int_C\f{3z+2}{z^2+1}dz \ \ \ (C \te{は} z=i \te{を中心とした半径} R(R<2) \te{の円}) $$

▼ 解答

[解答]
被積分関数の特異点は $i$ と $-i$ だが, $i$ は $C$ の内部, $-i$ は $C$ の外部にある. よって, $$ I=\int_C\f{f(z)}{z-i}dz,\ \ f(z)=\f{3z+2}{z+i} $$ と書いてコーシーの積分公式を用いれば, $$ f(i)=\f{3i+2}{2i} =\f{1}{2\pi i}\int_C\f{f(z)}{z-i}dz =\f{I}{2\pi i} $$ となる. よって, $$ I=2\pi i f(i)=(3i+2)\pi. $$

例題
$$ I:=\int_C\f{\sin z}{z^2+1}dz $$ を求めよ. ただし, $C$ は円 $|z|=2$ とする.

▼ 解答

[解答]
$$ \f{1}{z^2+1}=\f{1}{2i} \le(\f{1}{z-i}-\f{1}{z+i} \ri) $$ であり, 特異点 $i,-i$ はいずれも $C$ の内部にあるので, $f(z):=\sin z$ に対して, コーシーの積分公式を用いると, $$\eq{ I & =\f{1}{2i}\int_C\f{\sin z}{z-i}dz -\f{1}{2i}\int_C\f{\sin z}{z+i}dz \\ & =\pi(\sin i-\sin(-i)) \\ & =2\pi \sin i \\ & =\pi i(e-e^{-1}). }$$

グルサの定理

証明

グルサの定理
$f(z)$ を領域 $A$ 上で正則な関数とする.
$z_0$ が閉曲線 $C$ の内部の点ならば, $n=0,1,2,\cd$ に対して, $$ f^{(n)}(z_0)=\f{n!}{2\pi i}\int_C \f{f(z)}{(z-z_0)^{n+1}}dz $$ が成り立つ.

▼ 証明

[証明]
数学的帰納法で示す.
$n=1$ のとき, 導関数の定義から, $$ f'(z_0)=\lim_{\D z\to 0}\f{f(z_0+\D z)-f(z_0)}{\D z} $$ である. ここで, 点 $z_0+\D z$ は $C$ の内部にあるように, $\D z$ を十分小さくとっておく.
$f(z_0+\D z),f(z_0)$ に対してコーシーの積分公式を用いれば, $\def\HS{\hspace{20pt}}$ $$\eq{ & \f{f(z_0+\D z)-f(z_0)}{\D z} \\ & \HS =\f{1}{\D z}\le\{ \f{1}{2\pi i}\int_C\f{f(z)}{z-(z_0+\D z)}dz -\f{1}{2\pi i}\int_C\f{f(z)}{z-z_0}dz \ri\} \\ & \HS =\f{1}{2\pi i\D z}\int_C\le\{ \f{f(z)}{z-z_0-\D z}-\f{f(z)}{z-z_0} \ri\} \\ & \HS =\f{1}{2\pi i}\int_C \f{f(z)}{(z-z_0-\D z)(z-z_0)} dz }$$ となる. この両辺を $\D z\to 0$ とすれば, $$ f'(z_0)=\f{1}{2\pi i}\int_C\f{f(z)}{(z-z_0)^2} dz $$ を得られる. したがって, $n=1$ のときに等式は成り立つ.

同様に「$n=k$ のときに成り立つことを仮定して, $n=k+1$ のときに成り立つ」$\cd (*)$ ことを示せる.
よって, 帰納法より定理を証明できた.

[補足]
$(*)$ を示す.
$n=k$ のとき, すなわち $$ f^{(k)}(z_0)=\f{k!}{2\pi i} \int_C\f{f(z)}{(z-z_0)^{k+1}} dz $$ が成り立つことを仮定すると, $$\eq{ & \f{f^{(k)}(z_0+\D z)-f^{(k)}(z_0)}{\D z} \\ & \HS =\f{1}{\D z}\le\{ \f{k!}{2\pi i}\int_C\f{f(z)}{(z-z_0-\D z)^{k+1}}dz -\f{k!}{2\pi i}\int_C\f{f(z)}{(z-z_0)^{k+1}}dz \ri\} \\ & \HS =\f{k!}{2\pi i\D z}\int_C\le\{ \f{f(z)}{(z-z_0-\D z)^{k+1}}-\f{f(z)}{(z-z_0)^{k+1}} \ri\} \\ & \HS =\f{k!}{2\pi i\D z}\int_C \f{f(z)(k+1)(\D z)(z-z_0)^k+o}{(z-z_0-\D z)^{k+1}(z-z_0)^{k+1}} dz \\ & \HS =\f{(k+1)!}{2\pi i}\int_C \f{f(z)+o_0}{(z-z_0-\D z)^{k+1}(z-z_0)} dz }$$ (ただし, $o$ は $\D z$ の指数が２次以上の項の総和で, $o_0$ は $\D z$ の指数が１次以上の項の総和とする.)
この両辺を $\D z\to 0$ とすれば $$ f^{(k+1)}(z_0)=\f{(k+1)!}{2\pi i} \int_C\f{f(z)}{(z-z_0)^{k+2}} dz $$ を得られる.
よって $n=k+1$ のときに成り立つことを示せた.

グルサの定理を証明したと同時に, 正則関数は無限回微分可能であることも示している.

系
正則関数は無限回微分可能である.

また, グルサの定理によって, $\ds\int_C\f{f(z)}{(z-z_0)^{n+1}}dz$ の形の積分が計算できる.

例題

例題
積分 $\ds\int_{|z|=1}\f{e^{iz}}{z^3}dz$ の値を求めよ.

▼ 解答

[解答]
$f(z)=e^{iz}$ とおくと $f(z)$ は複素平面全体で正則であり, 点 $z=0$ は円 $|z|=1$ の内部にある. $$ f''(z)=i^2e^{iz}=-e^{iz} $$ であるから, グルサの定理によって, 求める積分の値は次のようになる. $$ \int_{|z|=1}\f{e^{iz}}{z^3}dz =\f{2\pi i}{2!}f''(0)=\f{2\pi i}{2}\c(-1)=-\pi i $$

例題
積分 $\ds\int_{|z|=1}\f{(z+i)^3}{z^4}dz$ の値を求めよ.

▼ 解答

[解答]
$f(z)=(z+i)^3$ とおくと $f(z)$ は複素平面全体で正則であり, 点 $z=0$ は円 $|z|=1$ の内部にある. $$ f''(z)=6(z+i)$$ であるから, グルサの定理によって, 求める積分の値は次のようになる. $$ \int_{|z|=1}\f{(z+i)^3}{z^4}dz =\f{2\pi i}{3!}f''(0)=\f{2\pi i}{6}\c(6i)=-2\pi $$

コーシーの積分公式の逆

次の定理のとおり, コーシーの積分公式の逆が成り立つ.

定理
$f(z)$ を領域 $D$ 上の連続関数とする. 任意の $z\in D$ に対して, $$ f(z)=\f{1}{2\pi i}\int_{\d\D} \f{f(\zeta)}{\zeta -z}d\zeta $$ が成り立つとする. ただし, $\D$ は $\ol{\D}\sub D$ を満たす中心 $z$ の開円板とする.
このとき, $f(z)$ は $D$ 上正則である.

▼ 証明

[証明]
開円板 $\D$ の半径を $r$ とする. $\d\D$ はコンパクトなので, $\d\D$ 上の連続関数 $f(z)$ は最大値を持つ. すなわち, $$ f(\z) \leq M\ \ \ (\z \in \d\D) $$ を満たす $M >0$ が存在する.
$h\in \C$ を $|h|\leq \f{r}{2}$ を満たすようにとると, $z+h\in \D$ である.

恒等式 $$ \f{1}{\z-(z+h)}-\f{1}{\z-z} =\f{h}{(\z-z)^2}+ \f{h^2}{(\z-(z+h))(\z-z)^2} $$ を用いると, $$\eq{ f(z+h)-f(z) & =\f{1}{2\pi i}\int_{\d\D} \le( \f{1}{\z-(z+h)}-\f{1}{\z-z} \ri)f(\z)d\z \\ & =\f{h}{2\pi i}\int_{\d\D} \f{f(\z)}{(\z-z)^2}d\z \\ & \ \ \ +\f{h^2}{2\pi i}\int_{\d\D} \f{f(\z)}{(\z-(z+h))(\z-z)^2}d\z }$$ を得る. $\z\in \d\D$ に対して $$\eq{ |\z-z| & =r, \\ |\z-(z+h)| & =|(\z-z)+(-h)| \\ & \geq |\z-z|-|-h| \\ & \geq r-r/2 \\ & = \f{r}{2} }$$ が成立する. (※三角不等式を用いた.)
したがって, 基本不等式より $$\eq{ & \le| \f{f(z+h)-f(z)}{h}-\f{1}{2\pi i} \int_{\d\D}\f{f(\z)}{(\z-z)^2}d\z \ri| \\ = & \le| \f{h}{2\pi i}\int_{\d\D} \f{f(\z)}{(\z-(z+h))(\z-z)^2}d\z \ri| \\ \leq & \f{|h|}{2\pi}\int_{\d\D} \f{|f(\z)|}{|\z-(z+h)||\z-z|^2}|d\z| \\ \leq & \f{M|h|}{\pi r^3}\int_{\d\D}|d\z| \\ = & \f{Ml}{\pi r^3}|h| \ \ \ \ \ \le(|h|\leq \f{r}{2}\ri) }$$ が成立する. ただし, $l$ は曲線 $\d\D$ の長さとする. (※$l=2\pi r$.)
したがって, $h\to 0$ とすると, $$ f'(z)=\f{1}{2\pi i} \int_{\d\D}\f{f(\z)}{(\z-z)^2}d\z $$ ゆえに, $f(z)$ は点 $z$ で正則である.
$z$ は $D$ 上の任意の点なので, $f(z)$ は $D$ 上で正則である.