ローラン展開と留数【例題】

$$ \newcommand{\ub}[1]{\underbrace{#1}} $$

この記事では、ローラン展開と留数に関する例題を扱います。

ローラン展開

基本事項

例題の前にローラン展開の基本事項について確認する.

定理 (ローラン展開)
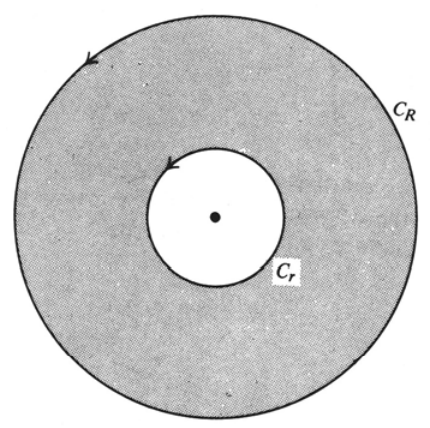$f(z)$ が $0<|z-c|< R$ で正則ならば, 任意の閉部分領域 $r_1 \leq |z-c| \leq r_2 (0 < r_1 < r_2 < R)$ で一様収束する級数 $$ f(z)=\sum_{n=-\iy}^\iy a_n (z-c)^n \ \ \ (0< |z-c| < R) \tag{*} $$ に展開できる. また係数 $a_n$ は $f(z)$ から一意的に定まり, $$ a_n=\f{1}{2\pi i}\int_{|\zeta-c|=r} \f{f(\zeta)}{(\zeta-c)^{n+1}}d\zeta $$ で与えられる. ただし, $r$ は $0< r< R$ を満たす任意の数である.

▼ 証明

[証明]
$c=0$ の場合を示せば, 一般の場合もただちに示せるので, $c=0$ の場合だけを示す.

（一意性）$f(z)$ が $(*)$ のように級数展開ができるとしよう. 任意の整数 $m$ をとり, $(*)$ の両辺に $z^{-m-1}$ を掛けて $|z|=r(0< r< R)$ で積分する. 収束の一様性から項別に積分ができるので $$ \oint_{|z|=r} f(z)z^{-m-1}\f{dz}{2\pi i} =\sum_{n=-\iy}^\iy a_n \oint_{|z|=r} z^{n-m-1}\f{dz}{2\pi i}=a_m. \tag{**}$$ 係数 $a_m$ は $f(z)$ だけを用いて書けているから一意的に定まる. 積分路変形の原理から $(**)$ は $r$ の値によらないことに注意しよう.

(存在)いま $r_1,r_2$ を $0< r_1 < r_2 < R$ となるように任意にとって固定し, $r_1 \leq |z| \leq r_2$ で考える. さらに $0 < R_1 < r_1, r_2 < R_2 < R$ として図の積分経路にコーシーの積分公式を適用すれば $$ f(z)=\oint_{|\z|=R_2}\f{f(\z)}{\z-z}\f{d\z}{2\pi i} -\oint_{|\z|=R_1}\f{f(\z)}{\z-z}\f{d\z}{2\pi i} $$ である. そこで, 被積分関数を
第１項： $$ \f{f(\z)}{\z-z}=\f{f(\z)}{\z\big(1-\tfrac{z}{\z}\big)} =\f{f(\z)}{\z}\sum_{n=0}^\iy \f{z^n}{\z^n} $$ 第２項： $$ -\f{f(\z)}{\z-z}=\f{f(\z)}{z-\z} =\f{f(\z)}{z}\sum_{n=0}^\iy \f{\z^n}{z^n} $$ と展開すれば, それぞれは $|\z|=R_2,\ |\z|=R_1$ で一様収束する. よって項別積分により, $$\eq{ f(z) & =\sum_{n=0}^\iy z^n \oint_{|\z|=R_2}f(\z)\z^{-n-1}\f{d\z}{2\pi i} +\sum_{n=0}^\iy z^{-n-1} \oint_{|\z|=R_1}f(\z)\z^n\f{d\z}{2\pi i} \\ & =\sum_{n=0}^\iy a_n z^n +\sum_{n=0}^\iy a_{-n-1}z^{-n-1} \\ & =\sum_{n=-\iy}^\iy a_n z^n. }$$ ただし, $(**)$ を使った. この展開は $r_1 \leq |z| \leq r_2$ で一様収束する.

定義
上式の級数 $$ \sum_{n=-\iy}^\iy a_n(z-c)^n $$ を $f(z)$ の点 $c$ に関するローラン展開(Laurent expansion)という.
また, $c$ を $f(z)$ の孤立特異点(isolated singular point)という.
ローラン展開の $z-c$ の負のベキの部分： $$ \sum_{n=-\iy}^{-1} a_n(z-c)^n =\cd + \f{a_{-3}}{(z-c)^3} + \f{a_{-2}}{(z-c)^2} + \f{a_{-1}}{z-c} $$ を孤立特異点 $C$ における $f(z)$ の主要部(principal part)という.

孤立特異点の分類

ローラン展開には次の三つの場合がある.

定義
(i)主要部がない場合, この場合には, $0< |z-c|< r$ のとき, $$ f(z)=a_0+a_1(z-c)+a_2(z-c)^2+\cd $$ であるから, $f(c)=a_0$ と定義すれば $f(z)$ は $c$ においても正則な関数となる. ゆえに, このとき, $c$ を $f(z)$ の除去可能特異点という.

(ii)主要部が有限級数, すなわち, $0< |z-c|< r$ のとき, $$ f(z)=\f{a_{-m}}{(z-c)^m}+\cd + \f{a_{-1}}{z-c} +\sum_{n=0}^\iy a_n(z-c)^n,\ \ (a_{-m}\neq 0) $$ である場合. この場合 $c$ を $f(z)$ の位数 $m$ の極(pole)という. $\sum_{n=-\iy}^\iy a_n(z-c)^n$ はすなわち $$ \cd + \f{a_{-n}}{(z-c)^n} + \cd + \f{a_{-1}}{z-c} +a_0+a_1(z-c)+a_2(z-c)^2+\cd $$
(ii)主要部が無限級数, すなわち無数の自然数 $n$ について $a_{-n}\neq 0$ である場合, この場合 $c$ を $f(z)$ の真性特異点(essential singular point)という.

例題

例題
$f(z)=e^{1/z}$ の $z=0$ に関するローラン展開の主要部を求めよ. また, それはどのような孤立特異点か.

▼ 解答

[解答]
$e^z$ の $z=0$ におけるテイラー展開は $$ e^z=1+z+\f{z^2}{2!}+\cd +\f{z^n}{n!}+\cd $$ なので, $e^{1/z}$ の $z=0$ におけるローラン展開は $$ e^{1/z}=\ub{\cd \f{1}{n!z^n}+\cd + \f{1}{2!z^2} +\f{1}{z}}_{\te{主要部}}+1 $$ である. 主要部は上記のとおりである.
主要部は無限の項からなるので $z=0$ は $e^{1/z}$ の真性特異点である.

例題
次の関数の孤立特異点 $z=0$ を中心とするローラン展開の主要部を求めよ.
また, それはどのような孤立特異点か.
$(1)\ \f{\sin z}{z}\ \ \ $ $(2)\ \f{e^z}{z^2}\ \ \ $ $(3)\ z^3\cos\f{1}{z}$

▼ 解答

[解答]
$(1)\ \f{\sin z}{z}$ のローラン展開は $$ \f{\sin z}{z} =1-\f{z^2}{3!}+\f{z^4}{5!}-\f{z^6}{7!}+\cd $$ なので, 主要部がない.
よって, $z=0$ は除去可能特異点である.

$(2)\ \f{e^z}{z^2}$ のローラン展開は $$ \f{e^z}{z^2} =\ub{\f{1}{z^2}+\f{1}{z}}_{\te{主要部}} +\f{1}{2!}+\f{z}{3!}-\f{z^2}{4!}+\cd $$ であり, 主要部は上記のとおりである.
よって, $z=0$ は位数２の極である.

$(2)\ z^3\cos\f{1}{z}$ のローラン展開は $$\eq{ z^3\cos\f{1}{z} & = z^3\le(1-\f{1}{2!z^2}+\f{1}{4!z^4} -\f{1}{6!z^6}+\f{1}{8!z^8}-\cd\ri) \\ & = \ub{\cd+\f{1}{8!z^5}-\f{1}{6!z^3} +\f{1}{4!z}}_{\te{主要部}}-\f{1}{2!}z+z^3 }$$ であり, 主要部は上記のとおりである.
よって, $z=0$ は真性特異点である.

留数

定義と性質

定義 (留数)
$0<|z-a|< R$ で正則な関数 $f(z)$ の $z=a$ におけるローラン展開を $$ f(z)=\sum_{n=-\iy}^\iy c_n(z-a)^n $$ とする. このとき 係数 $c_{-1}$ を $f(z)$ の $z=a$ における留数(residue)と呼び, $\Res(f(z),a)$ で表す.

定理 (極の位数と留数)
(1) 点 $a$ が $f(z)$ の位数 $k$ の極であるとき, $$ \Res(f(z),a)=\f{1}{(k-1)!} \lim_{z\to a}\f{d^{k-1}}{dz^{k-1}} \Big( (z-a)^kf(z) \Big) $$ 特に, 点 $a$ が $f(z)$ の位数１の極であるとき, $$ \Res(f(z),a)=\lim_{z\to a}(z-a)f(z) $$ (2) $f(z),g(z)$ が正則で $g(a)=0,g'(a)\neq 0$ のとき, $$ \Res\le(\f{f(z)}{g(z)},a\ri)=\f{f(a)}{g'(a)} $$

▼ 証明

[証明]
(1) 点 $a$ は $f(z)$ の位数 $k$ の極なので, $$ f(z)=\f{c_{-m}}{(z-a)^k}+\cd+\f{c_{-1}}{z-a} +c_0+c_1(z-a)+\cd $$ と表せる. これより, $$ (z-a)^kf(z)=c_{-k}+\cd+c_{-1}(z-a)^{k-1} +c_0(z-a)^k+ \cd $$ である. さらに, 両辺を $k-1$ 回微分すると, $$ \f{d^{k-1}}{dz^{k-1}}(z-a)^mf(z) =(k-1)!c_{-1}+k!c_0(z-a) +\cd $$ であるので, $$ \f{1}{(k-1)!}\lim_{z\to a}\f{d^{k-1}}{dz^{k-1}} (z-a)^kf(z)=c_{-1}=\Res(f(z),a). $$ 特に, $k=1$ のときは $$ \lim_{z\to a}(z-a)f(z)=\Res(f(z),a) $$ が成り立つ.

(2) $f(a)\neq 0$ のとき, 点 $a$ は $f(z)/g(z)$ の位数１の極なので, (1)の結果を用いると, $$\eq{ \Res\le(\f{f(z)}{g(z)},a\ri) & =\lim_{z\to a}(z-a)\f{f(z)}{g(z)} \\ & =\lim_{z\to a}\f{z-a}{g(z)-g(a)}f(z) \\ & =\f{f(a)}{g'(a)}. }$$ ※ $g(a)=0$ に注意.

例題

例題
$\ds f(z)=\f{1}{z^2-1}$ の極と留数を求めよ.

▼ 解答

[解答]
$f(z)$ の孤立特異点は $1,-1$ の２つであり, ともに位数１の極である. よって, $$\eq{ & \Res(f(z),1) =\lim_{z\to 1}(z-1)f(z) =\lim_{z\to 1}\f{1}{z+1} =\f{1}{2}, \\ & \Res(f(z),-1) =\lim_{z\to -1}(z+1)f(z) =\lim_{z\to -1}\f{1}{z-1} =-\f{1}{2}. }$$

例題
$\ds f(z)=\f{e^z}{(z-c)^3}$ の極と留数を求めよ.

▼ 解答

[解答]
$f(z)$ の孤立特異点は $z=c$ のみであり, これは位数３の極である. $$\eq{ \Res(f(z),c) & =\f{1}{2!}\lim_{z\to c}\f{d^2}{dz^2} \Big( (z-c)^3 f(z) \Big) \\ & =\f{1}{2}\lim_{z\to c}\f{d^2}{dz^2}(e^z) \\ & =\f{e^c}{2} }$$

例題
次の関数 $f(z)$ の極と留数を求めよ.
$\ds(1)\f{z}{e^z-1}\ \ \ (2) \f{1}{\sin^2z}$

▼ 解答

[解答]
(1) まず, 方程式 $e^z=1$ を解こう. $z=x+iy$ とすると, $$ e^z=e^{x+iy}=e^xe^{iy}=1 $$ より, $$ x=0,\ \ y=2n\pi\ \ (n\in \Z) $$ である. 従って, $f(z)$ の極は $$ 2n\pi i\ \ (n\in \Z,\ n\neq 0). $$ これらの留数は $$ \Res(f(z),2n\pi i)=\lim_{z\to 2n\pi i} \f{z}{(e^z-1)'}=2n\pi i. $$
(2) まず, 方程式 $\sin z=0$ を解こう. $z=x+iy$ とすると, $$ \sin z=\f{e^z-e^{-z}}{2i}=0 $$ より, $$\eq{ & e^x e^{iy}-e^{-x}e^{-iy}=0 \\ \iff & e^{2x}e^{2iy}=1 \\ \th & x=0, \ y=n\pi\ \ (n\in \Z) }$$ である. 従って, $f(z)$ の極は $$ n\pi i\ \ (n\in \Z). $$ 一方, $f(z)$ は偶関数なので, その留数は０である: $$ \Res(f(z), n\pi i)=0. $$

【付録】真性特異点の複雑性

次の定理が示すように, $z$ が真性特異点 $c$ に近づくときの $f(z)$ の変換はきわめて複雑である.

Weierstrassの定理
$c$ は $f(z)$ の真性特異点ならば, $c$ に収束する数列 $\{z_n\}$ を適当に選んで, 任意の $w\in \C$ に対して, $f(z_n)\to w(n\to \iy)$ となるようにできるし, $|f(z_n)|\to +\iy(n\to \iy)$ となるようにもできる.

この定理はつまり, 真性特異点への近づき方によって, $f(z)$ はどんな複素数にも収束させることもできるし, $\iy$ に発散させることもできることを言っている.
そのような例を述べる.

例
$$ f(z)=e^{1/z} =1+\f{1}{z}+\f{1}{2!z^2}+ \f{1}{3!z^3}+\cd $$ とおけば, $f(z)$ は $\C\sm\{0\}$ で正則な関数であり, 真性特異点 $0$ を持つ.

任意の $w\in \C\sm\{0\}$ が与えられたとき, $$ w=|w|e^{i\t},\ (\t\in \R) $$ とおけば, 任意の自然数 $n$ に対して $$ w=e^{\log|w|+i\t+2n\pi i} $$ である. ゆえに $z_n=1/(\log|w|+i\t+2n\pi i)$ とおけば, $0$ に収束する数列 $\{z_n\}$ で $f(z_n)=w$ なるものが得られる. この場合 $f(z_n)\to w\ (n\to \iy)$ であるだけでなく, $f(z_n)=w$ となる数列 $\{z\}$ が得られた.