Takatani Note

複素積分

$ \def\Re{\mathrm{Re}\hspace{1.2pt}} \def\all{\forall\ } $

この記事では, 複素平面上の曲線を定義したあと, 複素積分(複素関数の線積分)の定義と例を紹介します。

複素平面上の曲線

まず, 複素平面上の曲線を定義する.

曲線・閉曲線・単純

定義
複素数値の連続関数 $z:[a,b]\to \C$ のことを曲線(curve)という. (※$[a,b]$ は閉区間.)
曲線 $z(t)\ (a\leq t \leq b)$ を便宜上 $C$ で表すことが多い.

$z(a)$ を $C$ の始点, $z(b)$ を $C$ の終点という.
始点と終点が一致する(すなわち $z(a)=z(b)$ となる)曲線を閉曲線(closed curve)という.

曲線 $C$ が単純(simple)であるとは, 始点と終点を除いて $C$ が自分自身と交わったり重なったりしていないとき, すなわち $$ a\leq t_1 \neq t_2 < b \Longrightarrow z(t_1)\neq z(t_2) $$ が成り立っているときをいう.

単純な閉曲線のことを単純閉曲線という.

※曲線 $C$ が実関数 $x(t),y(t)$ によって, $$ z(t)=x(t)+iy(t)\ \ \ (a\leq t\leq b) \tag{*}$$ と表されるとき, $z(t)$ は連続関数なので, $x(t),y(t)$ も連続関数である.

※複素関数論では, パラメータ表示の仕方まで込めたもの, つまり複素数値の連続関数 $z(t)$ そのものを「曲線」と呼ぶ. たとえば, 次の３つの曲線は軌跡としては同じ円周になるが, 別の曲線として区別する.

※単純閉曲線として, 円周や長方形のような積分しやすい曲線がよく用いられる. 単純閉曲線の内側を左手に見るように周囲に向きをつけ, これを正の向きという. 円周ならば反時計回りの向きが正の向きである.

$-C$ と $C_1+C_2$

$(*)$ の曲線 $C$ に対して, 向きを逆にし, $z(b)$ を始点, $z(a)$ を終点とする曲線を記号 $-C$ によってあらわす. 式で書けば $$ -C : z=z(a+b-t) \ \ \ (a\leq t\leq b) $$ となる.

２つの曲線 $C_i:z=z_i(t) (a_i\leq t\leq b_i,\ i=1,2)$ において, $C_1$ の終点と $C_2$ の始点が一致しているならば (つまり $z_1(b_1)=z_2(a_2)$), はじめに $C_1$ の終点と $C_2$ の始点をつないだ曲線を考えることができる. これを $C_1+C_2$ で表す. すなわち, $$ C_1+C_2: z=\case{ z_1(t) & (a_1\leq t \leq b_1) \\ z_2(a_2+t-b_1) & (b_1 \leq t \leq b_1+b_2-a_2) }$$ である. いくつかの曲線をつなげたもの $C_1+\cd+C_r$ も同様に定義できる.

滑らかな曲線

応用上はあまり複雑な曲線は扱いにくいので, 条件をつけて考えたい.

定義
曲線 $C:z(t)=x(t)+iy(t)$ が滑らか(smooth)であるとは, $x(t),y(t)$ がともに $C^1$ 級であって, $$ (x'(t),y'(t))\neq (0,0) \ \ \ \ \ \ \ \ (\all t\in [a,b]) \tag{**}$$ が成り立つときをいう. ※条件 $(**)$ は曲線上の各点において接線が確定することを表す. (例えば, $(x(t),y(t))=(t^2,t^3)$ によって定まる曲線 $y^2=x^3$ は滑らかでない.)

定義
曲線 $C$ に対して, ある滑らかな曲線 $C_1,\cd,C_r$ があって $C=C_1+\cd+c_r$ と表せるとき, $C$ は区分的に滑らか(piecewise smooth)であるという.

当サイトではもっぱら区分的に滑らかな曲線のみを扱い, そのことをいちいち断らない. 私たちが念頭に置いているのは, 円周の一部や線分を有限個つないだ場合である.

複素積分

定義
$f(z)$ を領域 $D$ 上で定義された連続な複素関数とする. $C\sub D$ を滑らかな曲線とする. このとき, $f(z)$ の曲線 $C$ に沿った積分を $$ \int_C f(z) dz =\int_a^b f(z(t))\f{dz}{dt}dt \tag{*1}$$ で定義する.

また, 区分的に滑らかな曲線 $C=C_1+\cd+C_r$ については $$ \int_C f(z) dz = \int_{C_1} f(z) dz +\cd +\int_{C_r} f(z) dz \tag{*2}$$ によって定義する. 曲線 $C$ を積分経路という.

補足：複素線積分を上のように定義した理由について説明する.
実１変数の場合と同じように考えれば, 分点のとり方をどんどん細かくしていったときの区分和 $$ \sum_{i=0}^{N-1}f(z(t_i))\Big( z(t_{i+1}-z(t_i)) \Big)$$ の極限として複素積分を定義するのが自然だろう. $C$ が滑らかならば, この極限は存在して $(*)$ の右辺に収束することを示せる. (右辺は実変数の積分) しかし, ここでは極限の存在証明はせず, $C$ は滑らかなとき $(*1)$ を複素積分の定義に採用してしまうことにする.

例
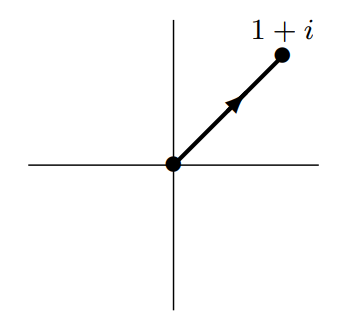$f(z)=x^2+iy^2$ とする. 線分 $C:z(t)=t+it\ (0\leq t\leq 1)$ を積分路にした積分 $\int_C f(z)dz$ を求めよ.

▼ 解答
[解答]
$z(t)=x(t)+iy(t)$ のように実部と虚部に分けると, $x(t)=y(t)=t$ である. したがって, $f(z(t))=t^2+it^2$ かつ $\dot{z}(t)=1+i.$ これより, $$ \int_C f(z) dz =\int_0^1 \le(t^2+i t^2\ri)(1+i)dt =\int_0^1 (1+i)^2 t^2 dt =\le[ 2i\f{t^3}{3} \ri]_0^1 =\f{2i}{3} $$

例
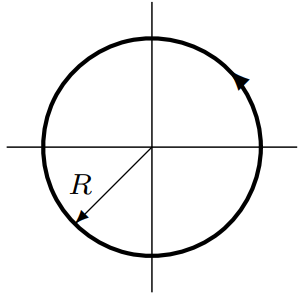$f(z)=1/z$ とする. このとき, 複素積分 $\int_C f(z)dz$ を求めよ. ただし, 曲線 $C$ は 半径 $R>0$ の円 $z(t)=Re^{2\pi it}\ $ $(0\leq t\leq 1)$ とする.

▼ 解答
[解答]
$f(z)=1/z$ に $z(t)=Re^{2\pi it}$ を代入すると, $$ f(z(t))=\f{1}{Re^{2\pi it}}. $$ また, $\dot{z}(t)=2\pi iR e^{2\pi it}$ なので, $$ \int_C f(z)dz =\int_0^1\f{2\pi iR e^{2\pi i t}}{Re^{2\pi it}}dt =2\pi i \int_0^1 dt=2\pi i. $$

複素積分の基本性質

複素積分の基本的な性質を列挙しよう. いずれも定義 $(*1),(*2)$ からすぐに確かめられる.

命題
$$\eq{ & \int_C (f(z)\pm g(z))dz =\int_C f(z)dz \pm \int_C g(z)dz, \\ & \int_C \a f(z)dz =\a \int_C f(z)dz, \\ & \int_{-C}f(z)dz =-\int_C f(z)dz, \\ & \int_{C_1+C_2}f(z)dz =\int_{C_1}f(z)dz + \int_{C_2}f(z)dz. }$$

複素積分の不等式

曲線の長さ

定義
区分的に滑らかな曲線 $z:[a,b]\to C$ を考える. いま $z(t)=x(t)+iy(t)$ と書く. そして, 写像 $z$ の像を $C$ とする. このとき, 曲線 $C$ の長さは $$ \int_C |dz|:=\int_a^b \le| \f{dz}{dt}(t) \ri| =\int_a^b \r{x'(t)^2+y'(t)^2}dt $$ である. この $\ds\int_C |dz|$ を拡張して次の積分を考える. 領域 $D$ 上の連続な複素関数 $f(z)$ と区分的に滑らかな曲線 $C\sub D$ をとる.

複素積分の不等式

定理
$$ \le| \int_C f(z)dz \ri| \leq \int_C |f(z)||dz|. $$ ここで右辺は, $C$ が $z=z(t)\ (a\leq t\leq b)$ と与えられるとき $$ \int_a^b |f(z(t))|\le| \f{dz}{dt} \ri| dt $$ を表す.

[証明]
積分の値を極形式で表示して $\int_C f(z)dz=Re^{i\t}$ とおく. この両辺に $e^{-i\t}$ を掛ければ実数になるから $$\eq{ \le| \int_C f(z)dz \ri| & =e^{-i\t}\int_C f(z)dz \\ & =\int_a^b \Re \le( e^{-i\t}f(z)\f{dz}{dt} \ri)dt \\ & \leq \int_a^b \le| e^{-i\t}f(z)\f{dz}{dt} \ri| dt \\ & = \int_a^b |f(z(t))|\le| \f{dz}{dt} \ri| dt. }$$