ジョルダンの補題【証明と応用】

$$ \newcommand{\zb}{\overline{z}} \def\all{\forall} \def\del{\delta} \def\tf{\tfrac} \def\Log{\mathrm{Log}\ } \def\Re{\mathrm{Re}\ } $$

この記事では,
・ジョルダンの補題
・ジョルダンの不等式
を証明します。これらは複素解析で積分を計算するときにしばしば用いられます。 その応用例も本記事で紹介します。

ジョルダンの不等式

まず, 次のジョルダンの不等式を証明する. この不等式はジョルダンの補題を証明するときに使う.

定理 (ジョルダンの不等式)
$0 < \t \leq \pi/2$ のとき, $$ \f{2}{\pi} \leq \f{\sin \t}{\t} \leq 1. $$

▼ 証明

[証明]
$$\lim_{\t\to 0}\f{\sin \t}{\t}=1 \ \te{かつ}\ \f{\sin(\pi/2)}{\pi/2}=\f{2}{\pi} $$ であるので, $f(\t):=\sin\t/\t$ が区間 $(0,\pi/2]$ 上で単調減少な関数であることを示せば十分である. $$ f'(\t)=\f{\t\cos\t-\sin\t}{\t^2} $$ であり, $F(\t):=\t\cos\t-\sin\t$ とおく. このとき, $$ F'(\t)=-\t\sin\t\leq 0 \ \ \ \ \ (\all \t\in [0,\pi/2]) $$ なので, $F(\t)$ は $[0,\pi/2]$ 上で単調減少な関数である. $F(0)=0$ より, $$ F(\t)\leq 0 \ \ \ \ \ (\all \t\in [0,\pi/2]) $$ が成り立つので, $$ f'(\t)\leq 0 \ \ \ \ \ (\all \t\in (0,\pi/2]) $$ を得る. よって, $f(\t)$ は $(0,\pi/2]$ 上で単調減少な関数である. これが示したいことであった.

ジョルダンの不等式の応用例を紹介する.

例題
$$ \int_0^\iy \cos(x^2)dx=\int_0^\iy \sin(x^2)dx =\r{\pi/8} $$

▼ 解答

[解答]
$\int_C \exp(iz^2)dz$ を考える. ただし, $C$ は下図のように角度 $\pi/4$ の円弧と２本の線分からなる閉曲線とする.

関数 $\exp(iz^2)$ は $C$ および $C$ 内で正則なので, コーシーの積分定理より $$\eq{ 0 & =\int_0^R \exp(ix^2)dx +\int_0^{\pi/4}\exp(iR^2e^{2i\t})iRe^{i\t}d\t -\int_0^R \exp (it^2e^{i\pi/2})e^{i\pi/4}dt \\ & =: I_1 +I_2 -I_3 }$$ いま, $$\eq{ |\exp(iR^2e^{2i\t}iRe^{i\t})| & =|R\exp (R^2(i\cos 2\t -\sin 2\t))| \\ & =R\exp(-R^2 \sin 2\t) \\ & \leq R \exp(-4R^2\t /\pi) \ \ \ \te{(ジョルダンの不等式より)} }$$ したがって $$\eq{ |I_2| & \leq R\int_0^{\pi/4}\exp(-4 R^2\t /\pi)d\t & = \f{\pi}{4R}(1-\exp(-R^2)) & \to 0\ \ \ (R\to \iy) }$$ ゆえに, $$ \int_0^\iy e^{ix^2}dx =\lim_{R\to \iy}I_3 =\f{1+i}{\r{2}}\int_0^\iy e^{-t^2}dt =(1+i)\r{\pi/8}. $$ よって, 上式の両辺について, 実数部分と虚数部分を比較すると, $$ \int_0^\iy \cos(x^2)dx=\int_0^\iy \sin(x^2)dx =\r{\pi/8}. $$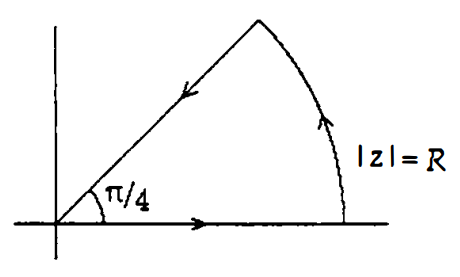

ジョルダンの補題

補題
$f(z)$ は有限個の点を除いて $\C$ 上正則で, 実軸上で連続な関数とする. さらに, $f(z)$ は ある $a>0$ と $g(z)$ によって $f(z)=e^{iaz}g(z)$ と表せるとする.

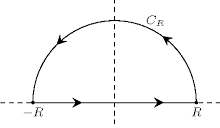
上図のとおり $C_R:=\{Re^{i\t} \mid 0\leq \t \leq \pi \}$ と定める. $\ds M_{R}:=\max_{\t \in [0,\pi]} \left|g\left(Re^{i\t }\right)\right|$ とする. このとき, 次の不等式が成り立つ. $$ \left|\int _{C_{R}}f(z)\,dz\right|\leq {\frac {\pi }{a}}M_{R}. $$

▼ 証明

[証明]
$$\eq{ \le|\int_{C_R}f(z)dz \ri| & =\le|\int_0^\pi g(Re^{i\t})e^{iaR(\cos\t +i\sin \t )}iRe^{i\t}d\t \ri| \\ & =R \le|\int_0^\pi g(Re^{i\t})e^{aR(i\cos\t -\sin \t )}ie^{i\t}d\t \ri| \\ & \leq R \int_0^\pi |g(Re^{i\t})|e^{-aR\sin\t )}ie^{i\t}d\t \\ & \ \ \ \ \ (\be |i|=|e^{i\t}|=|e^{iaR\cos\t}|=1) \\ & \leq RM_R\int_0^\pi e^{-aR\sin\t}d\t }$$ $\sin\t=\sin(\pi-\t)$ とジョルダンの不等式より $$\eq{ \int_0^\pi e^{-aR\sin\t}d\t & =2\int_0^{\pi/2} e^{-aR\sin\t}d\t \\ & \leq 2\int_0^{\pi/2} e^{-2aR\t/\pi}d\t \\ & = 2\le[ \f{\pi}{-2aR}e^{-2aR\t/\pi}\ri]_0^{\pi/2} \\ & =\f{1}{R}\c\f{\pi}{a}(1-e^{-aR}) }$$ よって, $$\eq{ \le|\int_{C_R}f(z)dz \ri| & \leq RM_R\int_0^\pi e^{-aR\sin\t}d\t \\ & \leq \f{\pi}{a}(1-e^{-aR})M_R \\ & \leq \f{\pi}{a}M_R. }$$

注意： ジョルダンの補題より, $R\to \iy$ のとき, $M_R \to 0$ ならば, $$ \lim_{R\to \infty }\int_{C_R}f(z)dz=0 $$ が成り立つ. この事実を定積分の計算で用いる.

問題
次を示せ. $$ \int_0^\iy \f{\sin x}{x}dx =\f{\pi}{2} $$

▼ 解答

[解答]

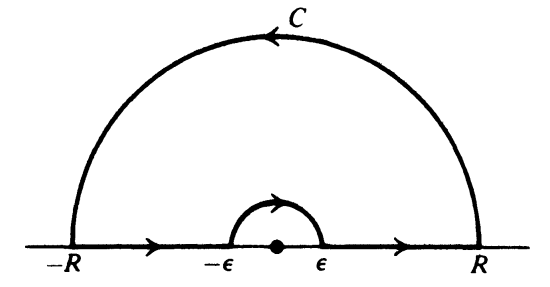
$f(z) =\f{e^{iz}}{z}$ とし, $0 < \e < R$ を満たすような実数 $\e,R$ をとる. 図のような単純閉曲線 $C$ を考え, $C_\e, C_R$ をそれぞれ半径 $\e$ の半円, 半径 $R$ の半円とする. $f(z)$ は原点以外において正則であるから、コーシーの積分定理により, $$ \int_C f(z)dz=0 $$ すなわち, $$ \int_{C_R} f(z)dz + \int_{-R}^{-\e} f(x)dx + \int_{C_\e} f(z)dz + \int_\e^R f(x)dx =0 \tag{*} $$ が成り立つ. これから, 左辺の各積分について考える.
まず, 左辺の第2項と第4項の和はオイラーの公式により $$\eq{ \int_{-R}^{-\e} \f{e^{ix}}{x}dx + \int_\e^R \f{e^{ix}}{x}dx & = -\int_\e^R \f{e^{-ix}}{x}dx + \int_\e^R \f{e^{ix}}{x}dx \\ & =2i \int_\e^R \f{\sin x}{x}dx \\ & =2i \int_0^\iy \f{\sin x}{x}dx \ \ \ ( \e\to 0, \ R\to \iy ) }$$ 次に, ジョルダンの補題より, 左辺の第１項は $R\to \iy$ のとき $0$ に収束する.

次に, 小半円の積分は $\e \to 0$ の極限で $$ \int_{C_\e}f(z)dz =\int_\pi^0 \f{e^{i\e e^{i\t}}}{\e e^{i\t}}i\e e^{i\t}d\t =-i\int_0^\pi e^{i\e e^{i\t}}d\t \to -i\pi $$ となる.
以上から, 式 $(*)$ に対して極限 $\e \to 0,\ R \to \iy$ をとれば $$ \int_0^\iy \f{\sin x}{x}dx =\f{\pi}{2} $$ を得る.

補足：ジョルダンの補題を使わないで, 左辺の第１項が $R\to \iy$ のとき $0$ に収束することの証明は下記のとおり.
置換 $z=Re^{it}(0\leq t \leq \pi)$ より, $$\begin{aligned}\left|\int _{C_{R}}f(z)\,dz\right|&=\left|\int _{0}^{\pi }f(Re^{it})iRe^{it}dt\right|\\&\leq \int _{0}^{\pi }|f(Re^{it})|R\,dt=\int _{0}^{\pi }e^{-R\sin t}dt=2\int _{0}^{\frac {\pi }{2}}e^{-R\sin t}dt\\&\leq 2\int _{0}^{\frac {\pi }{2}}e^{-2Rt/\pi }dt\quad \left(\because \ \ t\in \left[0,{\dfrac {\pi }{2}}\right]\ \Longrightarrow \ {\dfrac {2}{\pi }}t\leq \sin t\right)\\&={\frac {\pi }{R}}(1-e^{-R})\to 0\quad (R\to \infty ).\ \ \cdots (3)\end{aligned} $$